Binnen de fotografie is er geen getal zo belangrijk als het zogenaamde f/getal. Dit is een serie (op het oog willekeurige) getallen die de grootte van het diafragma weergeven. Het is een logaritmische schaal die als volgt wordt weergegeven:
f/1 -> 1.4 -> 2 -> 2.8 -> 4 -> 5.6 -> 8 -> 11 -> 16 -> 22 -> 32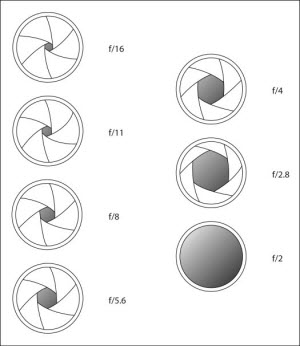
Op het eerste gezicht lijkt dit een reeks losstaande en willekeurige getallen. Gelukkig is er een ezelsbruggetje waarmee je deze serie vrij gemakkelijk kunt onthouden. En dat is erg belangrijk wanneer je snel een aanpassing wilt doen aan je belichting met behulp van je diafragma.
Wat maakt deze serie getallen nu zo speciaal?
De f/getallen in deze logaritmische serie worden ook wel hele stops genoemd. En wat het echt bijzonder maakt is dat ieder volgend getal precies tweemaal of de helft van het licht doorlaat als het voorgaande f/getal.
Bijvoorbeeld: f/5.6 laat precies tweemaal zoveel licht door als f/8. Dit betekent dat wanneer je fotografeert met f/5.6 en je wilt naar f/8 maar met dezelfde belichting, je ervoor moet zorgen dat de sluitertijd precies tweemaal zo lang wordt (omdat f/8 slechts de helft licht doorlaat als f/5.6). Stel dat je fotografeert op 1/100s op f/5.6, dan zul je bij f/8 naar een sluitertijd van 1/50s toe moeten.
Wanneer je nu deze reeks f/getallen uit je hoofd kent oftewel kunt dromen, dan kun je veel sneller en gemakkelijk switchen tussen f/getallen en de nieuwe bijbehorende sluitertijd kunnen berekenen.
Wellicht heeft jouw camera ook nog tussenliggende f/getallen die tussen de hele stops in liggen. Gewoonlijk in stapjes van een halve of een derde stop. Dus ook hier geldt: ken je de reeks hele stops, dan weet je ook wat je moet doen bij de tussenliggende stops.
Waar komt zo’n vreemde reeks vandaan?
Het f/getal is de verhouding tussen het brandpuntsafstand en de diameter van het diafragma: f/getal = (brandpuntsafstand) gedeeld door (diafragma diameter)
Bijvoorbeeld: je fotografeert met een 100mm lens (dat is het brandpuntsafstand) en de diameter (doorsnede) van het diafragma is 25mm, dan ik het f/getal 4 (100/25). In eerste instantie zou je denken dat het verdubbelen van de diafragma diameter ook tweemaal zoveel licht zou doorlaten. Maar dat is niet het geval, want het verdubbelen van de diafragma diameter geeft meer dan een verdubbeling van het oppervlaktegebied van het diafragma.
Het is het oppervlaktegebied van het diafragma dat verdubbeld moet worden om tweemaal zoveel licht door te laten. Om dat de bereiken moet je de diameter van het diafragma vermenigvuldigen met de wortel van 2, dat is ongeveer 1.414; en dat is meteen de reden waarom hele stops met stapjes van factor 1.414 lopen!
2.8 = 2.0 * 1.414
4 = 2.8 * 1.414
5.6 = 4 * 1.414
…en zo gaat het verder…
Verwarrend, nietwaar?
Een ezelsbruggetje om de reeks f/getallen te kunnen onthouden is dat de getallen steeds om en om verdubbelen. Kijk maar eens naar de vetgedrukte f/getallen:
f/1 -> 1.4 -> 2 -> 2.8 -> 4 -> 5.6 -> 8 -> 11 -> 16 -> 22 -> 32
f/1 -> 1.4 -> 2 -> 2.8 -> 4 -> 5.6 -> 8 -> 11 -> 16 -> 22 -> 32
Misschien helpt je dat om de reeks wat gemakkelijker van buiten te leren.
Om het ook even met een visueel voorbeeld duidelijk te maken zie je hieronder twee foto’s.
Wijd open diafragma, laag f-getal, veel licht door de lens, kleine scherptediepte
Ver gesloten diafragma, hoog f-getal, weinig licht door de lens, grote scherptediepte
Hieronder vind je een korte uitleg over wat diafragma is en doet uit de cursus Basiskennis Fotografie:
Ik begrijp dat dit misschien wel de eerste keer is dat je wiskunde gerelateerd ziet aan fotografie, dus als je iets niet volgt, laat het dan even weten in een reactie hieronder!
En voor wie dit teveel tekst is en voor de visueel ingestelden heb ik het in dit filmpje ook nog eens uitgelegd. Deze video is al veel eerder gemaakt en hoort niet persé bij dit artikel. Sterker nog, het is één van mijn eerste video’s, dus niet lachen! 😉
Weg van de Automatische stand op je camera
Belichting en de camera instellen
Richting van het licht, hoe fotografeer je dan?
Creatief belichten voor bijzondere foto’s
Belichting voor de beginner
Je heb je beroep misgelopen 🙂 je had leraar moeten worden..
Duidelijke uitleg!!
Hoi Peter, Ik krijg het filmpje niet geopendvan de diafragma’s.
Gr. Annemarie Vriends
Vreemd, deze staat gewoon open op Vimeo. Ik kan het wel zien in elk geval.
Ik ook niet kun je de link van vimeo sturen ?
mooie en duidelijke uitleg TOP!
volgende ISO?
Je staat er goed op!
Bedankt voor je duidelijke uitleg!
Complimenten voor het filmpje, dat zegt zoveel meer dan een grote lap tekst.
Dank voor jullie reacties, ik ben blij dat de video een beetje in de smaak gevallen is. Altijd lastig om in te schatten als je nooit voor de camera staat.
Misschien moet ik toch maar eens nadenken over een webinar/workshop/cursusdag… 😉
Jammer van het foutje in je video bij het rijtje van de diafragma’s.
Bij de laatste maak je een sprong van twee stops en sla je f45 over
verder kan het niet duidelijker!
Dank voor je reactie en toevoeging John!
Peter,
Om mee te beginnen: Prima en duidelijk uitgelegd.
Twee kleine dingen. In je voorbeeld heb je het over een sluitertijd van 1/400 -> 1/200 -> 1/100 maar die komen in het eindrijtje van jou niet voor.
Verder hebben camera’s ook nog zgn. tussenstops in het diafragma zoals b.v. F 6.3, F 7.1, F 9 etc.
Misschien ‘handig’ om dat in ieder geval te melden in je video?
Geweldige uitleg van 11.34sec.!
Dankjewel Mel!
Peter, goede uitleg. 1 dingetje echter, volgens mij is de reeks diafragmagetallen geen logaritmische reeks. Logaritmisch zou een machtsverheffing inhouden met een bepaald grondtal. Er zit weliswaar een macht van -2 (wortel) maar dat maakt het m.i. nog niet logaritmisch. Ik ben weliswaar geen wiskundige en ben er dus niet 100% zeker van maar kijk het voor de zekerheid even na.
Veel succes met je serie instructieblog en -video(s), Hans
Nu ben ik ook geen wiskundige, maar heb het wel altijd zo begrepen. Ik zal een kijken of ik het ergens kan vinden. Belangrijkste vind ik natuurlijk wel dat je het systeem van de lichtstops kent. De onderbouwing is ook weer niet aan iedereen besteed. Maar in elk geval dank voor je toelichting!
Peter, een goed verhaal zonder al te technisch te worden, bedankt!
Hans heeft wel een punt, logaritmisch (wanneer machten van x als ordegrootte worden gebruikt) is hier niet juist gebruikt. De boodschap is echter wel duidelijk en ik zou het zeker laten zoals het is.
Mocht je het interessant vinden: Als de schaal x={0, 1, 2, 3, 4, 5, 6, etc} zou zijn en dit zou staan voor 1.414 tot de macht x, dan zou het een logaritmische schaal zijn.
Hier is er sprake van een lineair verband met een factor 1.4 (1.414). Dat is, zoals jij correct uitlegt, omdat de diafragma opening cirkelvormig is en dus een oppervlakte heeft. Een oppervlakte is tweedimensionaal. Wanneer nu de doorsnede (of straal) van een cirkel 1.414 maal groter wordt, wordt het oppervlakte 1.414² = 1.414*1.414 = 2 maal zo groot (opp cirkel is π*r²). Daar ligt dan ook de verklaring waarom de stap naar vier keer meer licht een factor 2 is in het f-getal (2²=4).
Interessant is dat als het diafragma een vierkant, een driehoek of de vorm van een badeendje was geweest, hetzelfde principe nog steeds waar was.
Als laatste dan nog even waarom bij een lens (bijv 200mm f2.8) het maximale diafragmagetal halveert bij een 2.0 extender. De lens heeft nu eenmaal een maximale absolute diafragmaopening in millimeters(200mm/2.8=71.4mm). Wanneer je nu de brandpuntsafstand verdubbeld, resulteert dit in een f-getal dat dubbel zo groot is(400mm/71.4mm=5.6). Maar de absolute diafragmaopening is nog net zo groot….
Richard, je schrijft :”Daar ligt dan ook de verklaring waarom de stap naar vier keer meer licht een factor 2 is in het f-getal (2²=4).”. Dat klopt natuurlijk. Wel moest ik even nadenken waarom, als je bijv van f/2.0 naar f/2.8 gaat, de hoeveelheid licht niet verdubbelt, maar halveert. Ik begreep dat pas, nadat ik me realiseerde dat de de wortel2 onder de breukstreep staat (met de brandpuntsafstand erboven). Dat bedoel jij ook, natuurlijk, maar was mij niet direct duidelijk. Dit is gewoon ter info, niet bedoeld als kritiek. Peter (een andere).
hallo Peter
is er ook een formule voor een berekening van de iso , diafragma en de sluitertijd.
groetjes truus
Je bedoelt voor de lichtmeting in totaal? Nee, dat is ‘intelligentie’ die de camera vanuit de fabriek meekrijgt.
Truus, Peter,
natuurlijk kan dit en met de intelligentie van de camera heeft dit niets te maken. Momenteel ben ik bezig met de natte plaat (collodium) en die heeft ook een iso waarde ( tussen 1 & 2) deze werden vroeger gebruikt in houten camera’s zonder enige elektronica (intelligentie)
Een verdubbeling van de ISO/ASA waarde betekent dat de film half zoveel licht nodig heeft om een goed belicht beeld te geven.
Zie ook http://nl.wikipedia.org/wiki/Filmgevoeligheid
Groet, John
John, ik doelde op de formule van lichtmeting: wat is de ideale belichting.
De waarden van diafragma, sluitertijd en ISO worden uitgedrukt in stops die onderling inwisselbaar zijn, dat wordt hierboven (in het filmpje) uitgelegd.
Peter,
het filmpje is “erg duidelijk misschien begrijp ik de vraag niet.
Misschien dat Truus een aanvulling op de vraag kan geven om duidelijkheid te verschaffen.
John
Ja, ik denk dat we nog wat toelichting van Truus nodig hebben om een duidelijk beeld van de vraag te krijgen.
Kun je dat nog wat verder toelichten, Truus?
Bedankt voor de goede uitleg. Ik versta het nu al wat beter. Nu goed proberen vanbuiten te kennen en alles zal nu beter gaan. Ik had heel wat problemen met mijn sluitertijd en hopelijk zal het nu beter gaan met uw hulp.
Goed om te horen, Martine! Nu vooral veel DOEN. Nog een tip: schrijf of print deze getallenreeksen op een kaartje en stop die in je fototas (of wat dan ook). Mocht je het op enig moment niet meer weten, dan kun je altijd ter plaatse even ‘spieken’… 😉
Hallo Peter
Vaak gelezen over de getallen, nooit goed begrepen, bij je uitleg snap ik het zeker beter, ik kwam bij je omdat ik vanmiddag een fotoshoot maak van een gezin van 8 personen en dat buiten, nu wilde ik toch nog even de belichting checken….hier leer ik van ….ik had het al op papier maar vind het lastig te begrijpen
Dank je voor je uitleg
met een hartelijke groet Lia Smit
Dankjewel Lia, fijn om te lezen!
Hoi Peter,
Ik ben erg blij met jou super duidelijke uitleg. Gewoon in normale taal en in rustige stappen. Bedankt voor het delen van jou kennis en ik zal er nog weleens gebruik van maken! Begrijpen doe ik het wel maar onthouden….., maar dat heeft helaas een andere oorzaak.
Mvg, Rene
Fijn om te horen Rene. Ik hou niet van wollige taal of moeilijk doen. No nonsense is mijn credo. 🙂
Dit soort zaken moeten er vooral in slijten door het doen, dat werkt het beste. Hopelijk lukt dat ook bij jou, ik wens je het beste daarmee!
BestePeter,
vond vandaag je uitleg over f-waarden waar de diafragma opening in wordt uitgedrukt. Ik begrijp de verhouding tussen brandpunts afstand en openingsdiameter van het diafragma. Maar hoe zit dit bij een zoomlens?
Arie, bij een zoomlens veranderen die waarden steeds. Daarom is een zoomlens technisch gezien veel ingewikkelder en moeilijker te optimaliseren.
mijn 50mm 1.8 gaat als volg
1.8 – 2.0 – 2.2 – 2.5 – 2.8 – 3.2 – 3.5 – 4.0 – 4.5 – 5.0 – 5.6 – 6.3 – 7.1 – 8.0 – 9.0 – 10 – 11 – 13 – 14 – 16 – 18 – 20 – 22
en stopt op 22 alles klopt behalve bij 13 dan zou hij moeten stoppen op 26
Ferre: elke lens heeft een maximaal en minimaal diafragma. In jouw geval is de maximale opening f/1.8 en de minimale opening f/22. Er zijn wel lenzen die nog verder gaan, maar dat verschilt echt per lens.
Hoi Peter, leuke en vooral een duidelijke uitleg. Ik volg je al een poos en je houdt ook van een duidelijke uitleg. Niet moeilijker doen dan nodig1
Op o.a. FB kom je erg veel verwarring tegen wat betreft diafragma. Men praat vaak over een hoog of laag diafragma getal, of een groot / klein f-getal. Met een hoog of groot f-getal, bv f/22, wordt dan altijd een kleine opening bedoeld. Omdat men het zelf ook verwarrend vindt komt er dan nog de aanduiding bij ‘kleine opening’. In principe is het zo dat hoe groter het getal onder de streep, hoe kleiner het getal is. f/32 is echt een kleiner getal dan f/2. Dus behalve dat men verwarring zaait klopt het ook nog eens niet !! Allemaal verkeerd aangeleerd helaas.
Een OPENING kan klein of groot zijn, nooit hoog of laag. Een belichtingsTIJD kan kort of lang zijn. Nooit klein of groot.
Om het eenduidig te houden praat ik altijd over een groot of klein diafragma. Een belichtingstijd kort of lang.
ISO laag(gevoelig) of hoog(gevoelig). Wanneer je een bepaalde waarde wilt weten of instellen komen er getallen om de hoek kijken en dan is het idd erg makkelijk als je de reeks kent en wat het betekend voor de opening, tijd en gevoeligheid.
Dus jou uitleg is een genot om te lezen!!
Keep up the good work!!
grt van Raymond Schrave
Schrave Multi-Media.
Dank voor je mooie woorden Raymond!
Goede uitleg. Bedankt!
Nu fotografeer ik al vele tientallen jaren, maar er is één ding (en vermoedelijk volstrekt onbelangrijk) waarvan ik nooit de betekenis heb weten te achterhalen. En dat is de aanduiding 1: voorafgaand aan de cijfers voor de lichtsterkte van een objectief. Wat betekent toch die 1 met die dubbele punt? Is het een soort ‘grondgetal’ voor een denkbeeldige maximaal haalbare lensopening?
En… hoe tastbaar (bruikbaar) is het verschil tussen een 50mm 1.4 objectief en een 50mm 1.7 objectief. Ik werk met een Sony Alpha A900 en overweeg de tweedehands aankoop van zo’n Minolta/Sony objectief voor gebruik bij slechte lichtomstandigheden. Mijn andere twee zoom-objectieven kunnen niet groter dan 3.5 en 4.
Die 1: is eigenlijk de oorspronkelijke notatie. Vaak wordt het maximale diafragma van een lens aangeduid met bijvoorbeeld f/2.8 terwijl op de lens ook wel vermeld wordt: 1:2.8; Dat komt omdat het feitelijk een breuk is. Daarom is een diafragmaopening van f/2.8 ook groter dan die van f/16.
Beetje duidelijk zo?
Het verschil in lichtopbrengst tussen een 1.4 en een 1.8 lens is denk ik niet echt heel duidelijk merkbaar. Het gaat hier om 1/3 stop. Veel meer verschil zal waarschijnlijk zitten in het bokeh. Of dat dan het prijsverschil waard is, is voor iedereen weer een ander verhaal.
De lichtopbrengst bij f:1.4 is 70% meer dan bij f:1.8. T.o.v. f:2.0 zou het zelfs 100% zijn.
De hoeveelheid licht bij f:1.4 is te berekenen door 1/1.4 * 1/1.4= 0,51.
De hoeveelheid licht bij f:1.8 is te berekenen door 1/1.8 * 1/1.8 = 0,31
0.51 is t.o.v. 0,31 dus 70% meer.
Zie ook de uitleg in wikipedia: “diafragmagetal”.
Dank voor de info, maar ik denk dat dit voor de meesten niet meer te volgen is. Technisch allemaal heel correct, maar verre van eenvoudig en behapbaar.
Ook nu is dit filmpje nog steeds erg handig! Bedankt voor de uitleg en deze video voor altijd online laten staan 🙂
Ja, de inhoud is aardig tijdloos! Ik zal hem nog wel een poosje laten staan. 😉
beschouwen we het rijtje:
2.8 = 2.0 * 1.414
4 = 2.8 * 1.414
5.6 = 4 * 1.414
met diafragma 5.6 wordt in feite bedoeld 1/5.6
dus is misschien het volgende duidelijker:
1/5.6 * 1.414 = 1/4
1/4 * 1.414 = 1/2.8
enz.
ach muggezifterij…..dat weer wel.
Hoi Peter,
Ik heb een vraag en wellicht kan je mij helpen. Mijn belichtingsmeter kan ik wel instellen op 1/250 maar niet op 1/200 (voor zover ik weet) Echter mijn flitssynchronisatie is door mijn remote trigger max. 1/200. Als ik mijn belichtingsmeter op 1/250 instel, moet ik dan het diafragma 1/3 stop verder dichtdraaien ? (Kan alleen in derdes, niet in halven).
Alvast dank!
Groeten
Hans
De belichtingsmeter rekent nu met een iets kortere sluitertijd dan jij gebruikt en zal daarom een iets te open diafragma aangeven. Daarom zul je het diafragma iets verder dicht moeten zetten dan de belichtingsmeter aangeeft.
Ofwel: je gedachtengang klopt!
Exact berekend is de sluitertijd van de belichtingsmeter 1/4e korter dan die van de camera. Je zult dus zelf een keuze moeten maken hoe je dit verschil oplost in combinatie met je wens om iets lichtere of minder lichte opnames te maken.
“f” onderwerp goed uitgelegd!
Vraagje, wat zijn ideale parameters van de betere smartphone camera, voorbeeld… ?
Dankjewel Patrick!
Tja, wat zijn ideale parameters? Zijn er nog telefoons die slechte foto’s maken? Wil je de betere camera’s dan zit je toch al vrij snel in het wat duurdere segment. Verwacht van de goedkopere telefoons niet de beste foto’s. Zelf werken wij altijd met iPhones en zijn daar uitermate tevreden over.